Định lý Talet là một kiến thức rất quan trọng trong toán học được bổ sung vào chương trình học từ rất sớm và có ảnh hưởng lớn đến các môn học sau này. Qua bài viết dưới đây, chúng ta tìm hiểu định lý Talet trong tam giác và những hệ quả của định lý Talet.
Talet là gì?
Thalès de Milet theo phiên âm trong tiếng việt là Ta-lét là một nhà toán học người Hy Lạp. Trong nền triết học Hy Lạp cổ, ông được coi như là nhà triết gia đầu tiên – người đứng đầu trong bảy nhà hiền triết của Hy Lạp. Tên của ông được đặt cho một định lý toán học quan trọng mà ông đã phát hiện ra, chính là định lý Ta lét ngày nay.

Định lý Talet trong tam giác là gì?
Định lý Talet hay còn gọi là định lý Thales là một định lý có vai trò rất quan trọng trong hình học nói riêng và toán học nói chung. Định lý được đặt theo tên của nhà toán học Hy Lạp Thales de Milet. Định lý này hiện được giảng dạy ở tất cả các trường học và là một trong những kiến thức quan trọng mà học sinh nào cũng cần nắm chắc.
Định lý Talet trong tam giác
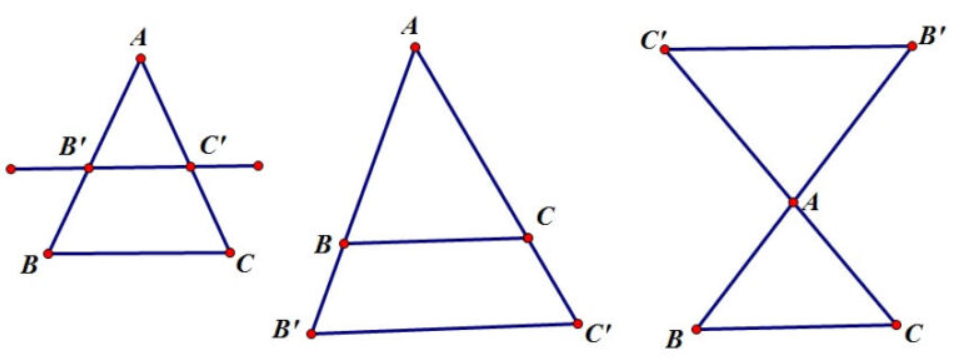
Định lý Talet thuận trong tam giác được phát biểu như sau: khi có một đường thẳng song song với một cạnh của tam giác đồng thời cắt hai cạnh kia thì nó sẽ xác định được các đoạn thẳng có tỉ lệ tương ứng trên hai cạnh đó cắt nhau.
Trong △ ABC, đoạn thẳng B’C ‘// BC thì ta sẽ có AB’/AB = AC’/AC
Định lý Talet đảo
Định lý Talet trong tam giác là một định lý gồm 2 chiều thuận và đảo
Định lý Talet nghịch đảo như sau: Nếu trong một tam giác, một đường thẳng cắt hai cạnh của tam giác đó và các đoạn thẳng xác định giao điểm của hai cạnh đó tỉ lệ với nhau thì đoạn thẳng đó sẽ song song nhau và song song với mặt còn lại.
Trong △ ABC, có AB’/AB = AC’/AC thì chúng ta sẽ có B’C ‘// BC.
Định lý Talet thuận và đảo trong tam giác có thể được áp dụng cho 3 trường hợp hình học như sau:
Những hệ quả của định lý Talet
Tiếp theo, chúng ta cùng phân tích ba hệ quả quan trọng của định lý Talet.
Hệ quả 1
Hệ quả đầu tiên của định lý Talet trong tam giác như sau: Một tam giác được tạo ra khi một đường thẳng song song với một cạnh của tam giác hiện có trong khi cắt hai cạnh còn lại. Ba cạnh mới tỉ lệ với ba cạnh của tam giác đã cho.
Trong △ ABC, đường thẳng DE // BC, chúng ta sẽ có: AD/AB = AE/AC = DE/BC
Đặc biệt, Hệ quả đầu tiên vẫn đúng đối với trường hợp đường thẳng a kéo dài cắt hai cạnh của tam giác đã cho và song song với cạnh còn lại.
Hệ quả 2
Hệ quả thứ hai của định lý Talet được biểu thị như sau: Khi 2 cạnh của một tam giác bị cắt bởi một đường thẳng và đường thẳng đó song song với cạnh còn lại của tam giác sẽ tạo ra một hình tam giác mới và tam giác mới đồng dạng với tam giác đã cho.
Hệ quả 3
Hệ quả 3 của định lý tam giác Talet còn được gọi là định lý Talet mở rộng. Định lý mở rộng phát biểu như sau: Khi ba đường thẳng song song, chúng sẽ cắt các cặp đoạn thẳng tỉ lệ trên hai đường thẳng song song.
Định lý Talet trong Hình thang
Ngoài định lý Talet trong hình tam giác, chúng ta cũng có thể áp dụng định lý Talet trong hình thang. Theo đó, định lý được phát biểu như sau: Khi trong hình thang, có một đường thẳng song song với hai cạnh đáy, đồng thời cắt cả hai cạnh của hình thang thì nó sẽ xác định một đoạn thẳng ở cả hai cạnh.
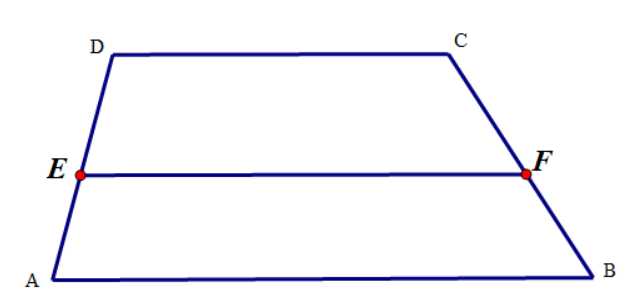
Ví dụ, trong hình thang ABCD có điểm E nằm trên đoạn AD và F nằm trên đoạn BC. Nếu đoạn thẳng EF // AB // CD thì ta sẽ có AE/DE = BF/CF và ngược lại, trong hình thang ABCD nếu ta AE/DE = BF/CF thì EF // AB // CD.
Định lý Talet trong không gian
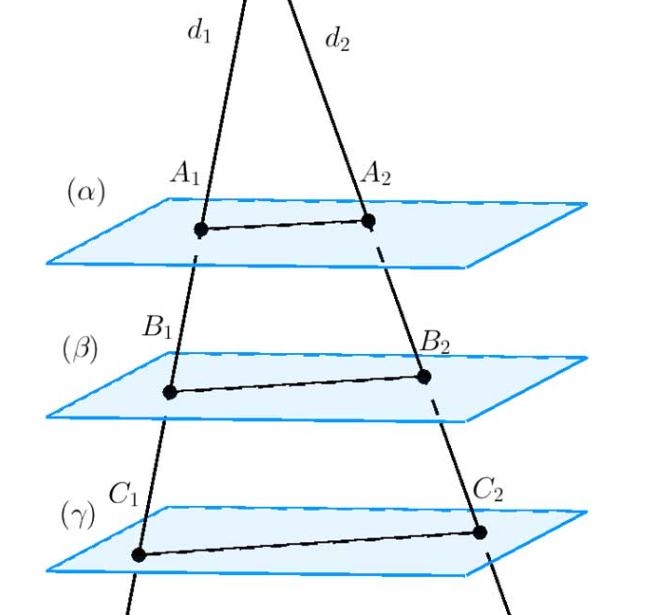
Định lý Talet cũng áp dụng cho hình học không gian. Trong không gian, định lý Talet phát biểu như sau: khi 3 mặt phẳng trong không gian song song sẽ chắn các đoạn thẳng có tỉ lệ tương ứng trên 2 đoạn thẳng.
Ngoài ra, người ta còn phát triển định lý nghịch đảo của định lý Talet trong không gian, được biểu diễn như sau: Với hai đường thẳng d1 và d2 chéo nhau các điểm A1, B1, C1 ∈ (d1) và A2, B2, C2 ∈ (d2 ) Khi đó các đường thẳng A1A2, B1B2, C1C2 sẽ song song với cùng một mặt phẳng.
Các ứng dụng của Định lý Talet
Ứng dụng của định lý Talet rất rộng rãi, đặc biệt khi đo các vật có kích thước quá lớn để đo trực tiếp. Định lý Talet được áp dụng trong hai ví dụ điển hình sau:
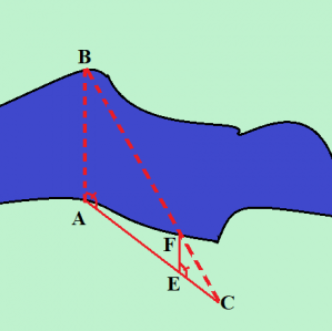
Đo khoảng cách giữa hai bờ sông mà không qua sông. Thay vì sử dụng thước đo kéo dài từ bờ sông bên này sang bờ bên kia thì ta có thể sử dụng định lý Talet để tính mà không cần qua sông. Ta tiến hành đo khoảng cách hai bờ sông như sau:
Bước 1: Gọi AB là đoạn thẳng mà ta cần đo, hai điểm A và B nằm ở 2 bờ sông. Chọn một điểm C bất kỳ.
Bước 2: Lấy E và F như hình sao cho EF//AB. Để xác định EF//AB ta cần đặt góc FEC bằng góc BAC.
Bước 3: Đo độ dài các đoạn EF, FC, AC sau đó tính AB theo công thức AB = (EF*AC) / FC
Thông qua độ dài của bóng do mặt trời chiếu xuống, ta có thể xác định chiều cao của một vật lớn.
Những dạng toán hay sử dụng định lý Talet
Trong toán học có nhiều dạng toán khác nhau có thể áp dụng định lý Talet để giải. Trong đó có các dạng tính chu vi của một đoạn thẳng, toán hình học hoặc dạng bài yêu cầu chứng minh các đường thẳng song song với nhau.

Dạng 1: Tính chu vi, diện tích, độ dài của đoạn thẳng và tính tỉ số của bài toán. Những dạng bài tập như thế này thường sử dụng định lý Talet, hệ quả định lý Talet cùng với những tỉ số đoạn thẳng. Về lý thuyết, nếu một đường thẳng cắt 2 cạnh của một tam giác và song song với cạnh còn lại thì có thể suy ra những đoạn thẳng có tỉ lệ tương ứng.
Dạng 2: Dạng bài chứng minh các đường thẳng song song hoặc chứng minh đẳng thức hình học. Dạng bài này thường áp dụng định lý Talet thuận, định lý đảo và các hệ quả của định lý để giải.
Như vật, bài viết trên đã tổng hợp những kiến thức chi tiết nhất về định lý Talet, hệ quả của định lý Talet, những ứng dụng và các dạng toán thường sử dụng định lý để giải. Hy vọng với những kiến thức đã chia sẻ, bạn có thể nắm bắt và vận dụng được định lý Talet trong học tập cũng như đời sống. Chúc bạn thành công!







